跳到主要内容

2.5 第二章复习

一、判断题（共5题，26分）​

  1. （判断题）（B）
∵x→0时sin⁡x~x∴lim⁡x→∞tan⁡x−sin⁡xsin⁡3x=lim⁡x→0x−xx3=0\Large \because x \rightarrow 0 \text{时} \sin x \text{\textasciitilde} x \\ \therefore \lim\limits_{x \rightarrow \infty} \frac{\tan x - \sin x}{\sin^3 x} = \lim\limits_{x \rightarrow 0} \frac{x - x}{x^3} = 0
  • A. 对
  • B. 错
  1. （判断题）（A）
lim⁡x→0xsin⁡1x=lim⁡x→0⋅lim⁡x→0sin⁡1x=0\Large \lim\limits_{x \rightarrow 0} x \sin \frac{1}{x} = \lim\limits_{x \rightarrow 0} · \lim\limits_{x \rightarrow 0} \sin \frac{1}{x} = 0
  • A. 对
  • B. 错
  1. （判断题）（A） 设 f(x)f(x) 在 [a,b][a, b] 上连续且无零点，则 f(x)f(x) 在上 [a,b][a, b] 恒为正或恒为负。
  • A. 对
  • B. 错
  1. （判断题）（A） 1x\Large \frac{1}{x} 是无穷小
  • A. 对
  • B. 错
  1. （判断题）（A） 当 x→0x \rightarrow 0 时，sin⁡3x\sin 3x 与 ex−1e^x - 1 是同阶无穷小。
  • A. 对
  • B. 错

二、简答题（共7题，36.4分）​

  1. （简答题） 求曲线 y=1∣x∣\Large y = \frac{1}{|x|} 的渐进线。
  1. （简答题） 设函数 f(x)={sin⁡2x∣x∣,当x<0−2,当x=02x2−2,当0<x≤1x,当x>1\Large f(x) = \begin{cases} \frac{\sin 2x}{|x|}, & \text{当} x < 0 \\ -2, & \text{当} x = 0 \\ 2x^2 - 2, & \text{当} 0 < x \leq 1 \\ x, & \text{当} x > 1 \\ \end{cases} ，讨论 f(x)f(x) 在 x=1x = 1 处的连续性。

解： 当 x=0x = 0 时：

lim⁡x→0−f(x)=lim⁡x→0−sin⁡2x∣x∣=2lim⁡x→0+f(x)=lim⁡x→0+2x2−2=−2lim⁡x→0−f(x)≠lim⁡x→0+f(x)\large \lim\limits_{x \rightarrow 0^-} f(x) = \lim\limits_{x \rightarrow 0^-} \frac{\sin 2x}{|x|} = 2 \\ \lim\limits_{x \rightarrow 0^+} f(x) = \lim\limits_{x \rightarrow 0^+} 2x^2 - 2 = -2 \\ \lim\limits_{x \rightarrow 0^-} f(x) \not= \lim\limits_{x \rightarrow 0^+} f(x) \\

即 f(x)f(x) 在 x≥0x \geq 0 处不连续。

当 x=1x = 1 时：

lim⁡x→1−f(x)=lim⁡x→1−2x2−2=0lim⁡x→1+f(x)=lim⁡x→1+x=1lim⁡x→1−f(x)≠lim⁡x→1+f(x)\large \lim\limits_{x \rightarrow 1^-} f(x) = \lim\limits_{x \rightarrow 1^-} 2x^2 - 2 = 0 \\ \lim\limits_{x \rightarrow 1^+} f(x) = \lim\limits_{x \rightarrow 1^+} x = 1 \\ \lim\limits_{x \rightarrow 1^-} f(x) \not= \lim\limits_{x \rightarrow 1^+} f(x) \\

即 f(x)f(x) 在 x=1x = 1 处不连续。

  1. （简答题） 设 f(x)f(x) 在 [a,b][a, b] 上连续，且 f(a)<a,f(b)>bf(a) < a, f(b) > b，
    证明：f(x)=xf(x) = x 在 (a,b)(a, b) 内至少有一个根。

解：

∵lim⁡x→01∣x∣=∞∴x=0为其垂直渐进线∵lim⁡x→∞1∣x∣=0∴y=0为其水平渐进线\large \because \lim\limits_{x \rightarrow 0} \frac{1}{|x|} = \infty \\ \therefore x = 0 \text{为�其垂直渐进线} \\ \because \lim\limits_{x \rightarrow \infty} \frac{1}{|x|} = 0 \\ \therefore y = 0 \text{为其水平渐进线}
  1. （简答题） 设函数 f(x)={x2+1,x<0x,x≥0\Large f(x) = \begin{cases} x^2 + 1, & x < 0 \\ x, & x \geq 0 \\ \end{cases} ，判断 lim⁡x→0f(x)\Large \lim\limits_{x \rightarrow 0} f(x) 是否存在。
  1. （简答题）求下列函数的间断点：

(1).f(x)=1(x+2)2\Large \text{(1).} f(x) = \frac{1}{(x + 2)^2}          (2).f(x)={sin⁡xx,x≠02,x=0\Large \text{(2).} f(x) = \begin{cases} \frac{\sin x}{x}, & x \not= 0 \\ 2, & x = 0 \\ \end{cases}

  1. （简答题） 设 lim⁡x→1x2+ax+bx2−1=3\Large \lim\limits_{x \rightarrow 1} \frac{x^2 + ax +b}{x^2 - 1} = 3 求 aa 和 bb。
  1. （简答题） 若 x→x0x \rightarrow x_0 时，α(x)\alpha(x) 与 α1(x)\alpha_1(x) 是等价无穷小， α(x)\alpha(x) 与 β(x)\beta(x) 是同阶无穷小，但不是等价无穷小， 证明：α(x)−β(x)\alpha(x) - \beta(x) 与 α1(x)−β(x)\alpha_1(x) - \beta(x) 也是等价无穷小。

解：

由原题得出：lim⁡x→x0α(x)β(x)=1,即lim⁡x→x0α(x)=lim⁡x→x0α(x)=lim⁡x→x0α1(x)∵lim⁡x→x0α(x)β(x)=A,A为常量且A∉{0,1}∴lim⁡x→x0α(x)≠lim⁡x→x0β(x)∴lim⁡x→x0α(x)−β(x)α(x)−β(x)=1\large \text{由原题得出：} \\ \lim\limits_{x \rightarrow x_0} \frac{\alpha(x)}{\beta(x)} = 1, \text{即} \lim\limits_{x \rightarrow x_0} \alpha(x) = \lim\limits_{x \rightarrow x_0} \alpha(x) = \lim\limits_{x \rightarrow x_0} \alpha_1(x) \\ \because \lim\limits_{x \rightarrow x_0} \frac{\alpha(x)}{\beta(x)} = A, A \text{为常量且} A \notin \{ 0, 1 \} \\ \therefore \lim\limits_{x \rightarrow x_0} \alpha(x) \not= \lim\limits_{x \rightarrow x_0} \beta(x) \\ \therefore \lim\limits_{x \rightarrow x_0} \frac{\alpha(x) - \beta(x)}{\alpha(x) - \beta(x)} = 1

三、计算题（共7题，37.6分）​

  1. lim⁡x→0+ln⁡(1+x3)⋅(1−cosx)arcsin⁡⋅(1−x3−1)\Large\lim\limits_{x\rightarrow 0^+}\frac{\ln(1+x^3)·(1-cos\sqrt{x})}{\arcsin·(\sqrt{1-x^3}-1)}

    题解

    在该极限中明显 X 趋于 0（无穷小），可直接根据无穷小转化公式

    ln⁡(1+x) x\ln(1+x) ~ x , 1−cos⁡x→(12)x2,arcsin⁡x→x1 - \cos x \to ( \frac{1}{2} ) x^2, \arcsin x \to x,

    1+xan−1→1nxa\sqrt[n]{1+x^a}-1 \to \frac{1}{n}x^a

    转化后原式：

    lim⁡x→0+x3⋅12(x)2x⋅12(−x3)=−1\Large\lim\limits_{x \to 0^+}\frac{x^3·\frac{1}{2}(\sqrt{x})^2}{x·\frac{1}{2}(-x^3)}=-1

  2. lim⁡x→0esin2x−esinxx\Large\lim\limits_{x\rightarrow 0}\frac{e^{sin2x}-e^{sinx}}{x}

    答案：

  3. lim⁡x→01−cos2xxsinx\Large\lim\limits_{x \rightarrow 0}\frac{1-cos2x}{xsinx}

    题解

    本题主要涉及第一重要极限：lim⁡x→0sinxx=1\lim\limits_{x \to 0}\frac{sinx}{x}=1

    要利用第一重要极限主要影满足 00\frac{0}{0} 型；② lim⁡sin()()=1\lim\limits\frac{sin()}{()}=1

    lim⁡x→01−cos2xxsinx=lim⁡x→02sin2xxsinx=2lim⁡x→0sinxx=2\begin{align*} & \lim\limits_{x \rightarrow 0}\frac{1-cos2x}{xsinx} \\ & = \lim\limits_{x \rightarrow 0}\frac{2sin^2x}{xsinx} \\ & = 2 \lim\limits_{x \rightarrow 0}\frac{sinx}{x} \\ & = 2 \end{align*}

  4. lim⁡x→1x2+2x−3x+3−2\Large\lim\limits_{x \rightarrow 1}\frac{x^2+2x-3}{\sqrt{x+3}-2}

    题解

    看到（任意）这个极限可以先将 x = 1代入原式明显极限为 00\frac{0}{0} 型，可用约去零因子法（注：课本p44详例），而又原式分母有根号，采用分母有理化。 原式：

    lim⁡x→1x2+2x−3x+3−2=lim⁡x→1(x2+2x−3)(x+3+2)(x+3−2)(x+3+2)=lim⁡x→1(x2+2x−3)(x+3+2)(x−1)=16\Large \begin{align*} & \lim\limits_{x \rightarrow 1}\frac{x^2+2x-3}{\sqrt{x+3}-2} \\ & = \lim\limits_{x \to 1}\frac{(x^2+2x-3)(\sqrt{x+3}+2)}{(\sqrt{x+3}-2)(\sqrt{x+3}+2)} \\ & = \lim\limits_{x \to 1}\frac{(x^2+2x-3)(\sqrt{x+3}+2)}{(x-1)} \\ & = 16 \end{align*}

  5. lim⁡x→∞(3+x6+x)x−12\Large\lim\limits_{x \to \infty }{(\frac{3+x}{6+x})}^\frac{x-1}{2}

    题解

    这题主要考察第二重要极限的运用：lim⁡x→∞(1+1x)x\lim\limits_{x \to \infty}(1+\frac{1}{x})^x

    要利用第一重要极限主要影满足 ① 1∞1^\infty 型；②lim⁡(1+【】)1【】=e\lim\limits(1+【】)^\frac{1}{【】}=e

    答案：

  6. lim⁡x→1x2−2x+1x2−1\Large\lim\limits_{x \to 1 }\frac{x^2-2x+1}{x^2-1}

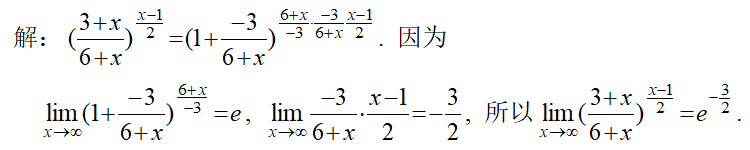
    题解

    看到（任意）这个极限可以先将 x = 1代入原式明显极限为 00\frac{0}{0} 型，可用约去零因子法

    原式：

    lim⁡x→1x2−2x+1x2−1=lim⁡x→1(x−1)2(x+1)(x−1)=lim⁡x→1x−1x+1=02=0\Large \begin{align*} &\lim\limits_{x \to 1 }\frac{x^2-2x+1}{x^2-1}\\ &=\lim\limits_{x \to 1 }\frac{(x-1)^2}{(x+1)(x-1)}\\ &=\lim\limits_{x \to 1 }\frac{x-1}{x+1}\\ &=\frac{0}{2}\\ &=0 \end{align*}

  7. lim⁡x→+∞1+x1−x\Large\lim\limits_{x \to +\infty}\frac{1+\sqrt{x}}{1-\sqrt{x}}

    题解

    这个极限可以先将 x = 1代入原式明显极限为 ∞∞\frac{\infty}{\infty} 型,分子分母同时除以 x 的最高次幂

    原式：

    lim⁡x→+∞1+x1−x=lim⁡x→+∞1x+11x−1常数除以无穷等于0=lim⁡x→+∞0+10−1=−1\Large \begin{align*} & \lim\limits_{x \to +\infty}\frac{1+\sqrt{x}}{1-\sqrt{x}}\\ & =\lim\limits_{x \to +\infty}\frac{\frac{1}{\sqrt{x}}+1}{\frac{1}{\sqrt{x}}-1} \text{常数除以无穷等于0} \\ & =\lim\limits_{x \to +\infty}\frac{0+1}{0-1}\\ & =-1 \end{align*}