定义 1
设 X , Y X, Y X , Y f f f X X X x x x f f f Y Y Y y y y f f f X X X Y Y Y 映射
f : X → Y f: X \to Y f : X → Y 其中 y y y x x x f f f 像 f ( x ) f(x) f ( x )
y = f ( x ) y = f(x) y = f ( x ) 而元素 x x x y y y f f f 原像 X X X f f f D f D_f D f D f = X D_f = X D f = X X X X f f f R f R_f R f f ( X ) f(X) f ( X )
R f = f ( X ) = { f ( x ) ∣ x ∈ X } R_f = f(X) = \{ f(x) \mid x \in X \} R f = f ( X ) = { f ( x ) ∣ x ∈ X } 定义 2
设数集 D ⊆ R D \subseteq \mathbf{R} D ⊆ R f : D → R f: D \rightarrow \mathbf{R} f : D → R D D D 函数
y = f ( x ) , x ∈ D y = f(x), \quad x \in D y = f ( x ) , x ∈ D 其中 x x x 自变量 y y y 因变量 D D D 定义域 D f D_f D f D f = D D_f = D D f = D
函数的定义中,对每个 x ∈ D x \in D x ∈ D f f f y y y f f f x x x 函数值 f ( x ) f(x) f ( x ) y = f ( x ) y = f(x) y = f ( x ) y y y x x x 函数关系 f ( x ) f(x) f ( x ) f f f 值域 R f R_f R f f ( D ) f(D) f ( D )
R f = f ( D ) = { y ∣ y = f ( x ) , x ∈ D } R_f = f(D) = \{ y \mid y = f(x), x \in D \} R f = f ( D ) = { y ∣ y = f ( x ) , x ∈ D }
常用简单函数及其定义域
函数 定义域 y = Q ( x ) P ( x ) y = \frac{Q(x)}{P(x)} y = P ( x ) Q ( x ) P ( x ) ≠ 0 P(x) \not = 0 P ( x ) = 0 y = x 2 n y = \sqrt[2n]{x} y = 2 n x x ≥ 0 x \ge 0 x ≥ 0 y = log a x y = \log_a x y = log a x x > 0 x > 0 x > 0 y = sin x y = \sin x y = sin x y = cos x y = \cos x y = cos x R \mathbf{R} R y = arcsin x y = \arcsin x y = arcsin x y = arccos x y = \arccos x y = arccos x ∣ x ∣ < 1 \vert x \vert < 1 ∣ x ∣ < 1 y = tan x y = \tan x y = tan x y = sec x y = \sec x y = sec x { x ∈ R ∣ x ≠ k π + π 2 , k ∈ Z } \{ x \in \mathbb{R} \mid x \neq k \pi + \frac{\pi}{2} , k \in \mathbb{Z} \} { x ∈ R ∣ x = kπ + 2 π , k ∈ Z } y = cot x y = \cot x y = cot x y = csc x y = \csc x y = csc x { x ∈ R ∣ x ≠ k π , k ∈ Z } \{ x \in \mathbb{R} \mid x \neq k \pi , k \in \mathbb{Z} \} { x ∈ R ∣ x = kπ , k ∈ Z }
Z \mathbb{Z} Z R \mathbb{R} R 实数 构成的集合;
函数的有界性
设函数 f ( x ) f(x) f ( x ) D D D X ⊆ D X \subseteq D X ⊆ D
如果存在数 K 1 K_1 K 1
f ( x ) ≤ K 1 f(x) \leq K_1 f ( x ) ≤ K 1 对任一 x ∈ X x \in X x ∈ X f ( x ) f(x) f ( x ) X X X 上界 K 1 K_1 K 1 f ( x ) f(x) f ( x ) X X X
如果存在数 K 2 K_2 K 2
f ( x ) ≥ K 2 f(x) \geq K_2 f ( x ) ≥ K 2 对任一 x ∈ X x \in X x ∈ X f ( x ) f(x) f ( x ) X X X 下界 K 2 K_2 K 2 f ( x ) f(x) f ( x ) X X X
如果存在正数 M M M
∣ f ( x ) ∣ ≤ M |f(x)| \leq M ∣ f ( x ) ∣ ≤ M 对任一 x ∈ X x \in X x ∈ X f ( x ) f(x) f ( x ) X X X 有界 M M M f ( x ) f(x) f ( x ) X X X 无界 M M M x 1 ∈ X x_1 \in X x 1 ∈ X ∣ f ( x 1 ) ∣ > M |f(x_1)| > M ∣ f ( x 1 ) ∣ > M f ( x ) f(x) f ( x ) X X X
函数的单调性
设函数 y = f ( x ) y=f(x) y = f ( x ) D D D I ⊆ D I \subseteq D I ⊆ D
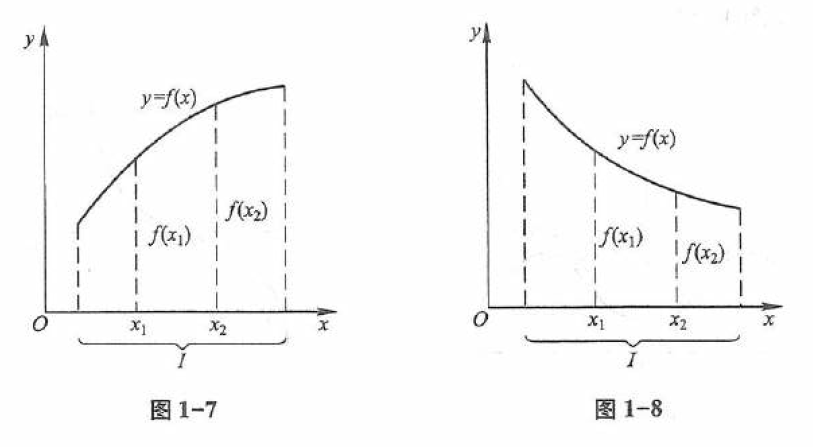
如果对于区间 I I I x 1 x_1 x 1 x 2 x_2 x 2 x 1 < x 2 x_1 < x_2 x 1 < x 2
f ( x 1 ) < f ( x 2 ) f(x_1) < f(x_2) f ( x 1 ) < f ( x 2 ) 那么称函数 y = f ( x ) y=f(x) y = f ( x ) I I I 单调增加的
如果对于区间 I I I x 1 x_1 x 1 x 2 x_2 x 2 x 1 < x 2 x_1 < x_2 x 1 < x 2
f ( x 1 ) > f ( x 2 ) f(x_1) > f(x_2) f ( x 1 ) > f ( x 2 ) 那么称函数 y = f ( x ) y=f(x) y = f ( x ) I I I 单调减少的
单调增加和单调减少的函数统称为 单调函数
函数的奇偶性
设函数 f ( x ) f(x) f ( x ) D D D
如果对于任一 x ∈ D x \in D x ∈ D
f ( − x ) = f ( x ) f(-x) = f(x) f ( − x ) = f ( x ) 恒成立, 那么称 f ( x ) f(x) f ( x ) 偶函数
如果对于任一 x ∈ D x \in D x ∈ D
f ( − x ) = − f ( x ) f(-x) = -f(x) f ( − x ) = − f ( x ) 恒成立, 那么称 f ( x ) f(x) f ( x ) 奇函数
奇函数的函数图像是 原点对称 或 中心对称 的,
偶函数的函数图像是 轴对称 的。
偶函数 × 偶函数 = 偶函数
简单地说就是,
具有相同奇偶性的函数的乘积为偶函数;
具有不同奇偶性的函数的乘积为奇函数。
函数的周期性
设函数 f ( x ) f(x) f ( x ) D D D l l l x ∈ D x \in D x ∈ D ( x ± l ) ∈ D (x \pm l) \in D ( x ± l ) ∈ D
f ( x + l ) = f ( x ) f(x+l) = f(x) f ( x + l ) = f ( x ) 恒成立,那么称 f ( x ) f(x) f ( x ) 周期函数 l l l f ( x ) f(x) f ( x ) 周期 周期 函数的周期是指 最小正周期
反函数
设函数 f : D → f ( D ) f: D \rightarrow f(D) f : D → f ( D ) f − 1 : f ( D ) → D f^{-1}: f(D) \rightarrow D f − 1 : f ( D ) → D f − 1 f^{-1} f − 1 f f f 反函数
按此定义,对每个 y ∈ f ( D ) y \in f(D) y ∈ f ( D ) x ∈ D x \in D x ∈ D f ( x ) = y f(x) = y f ( x ) = y
f − 1 ( y ) = x f^{-1}(y) = x f − 1 ( y ) = x 这就是说,反函数 f − 1 f^{-1} f − 1 f f f
复合函数
复合函数是复合映射的一种特例,按照通常函数的记号,复合函数的概念可如下表述:
设函数 y = f ( u ) y=f(u) y = f ( u ) D f D_f D f u = g ( x ) u=g(x) u = g ( x ) D g D_g D g R g ⊆ D f R_g \subseteq D_f R g ⊆ D f
y = f [ g ( x ) ] , x ∈ D g y = f[g(x)], \quad x \in D_g y = f [ g ( x )] , x ∈ D g 称为由函数 u = g ( x ) u=g(x) u = g ( x ) y = f ( u ) y=f(u) y = f ( u ) 复合函数 D g D_g D g u u u 中间变量
函数的运算
设函数 f ( x ) , g ( x ) f(x), g(x) f ( x ) , g ( x ) D f , D g , D = D f ∩ D g ≠ ∅ D_f, D_g, D = D_f \cap D_g \neq \varnothing D f , D g , D = D f ∩ D g = ∅
和(差)f ± g f \pm g f ± g
( f ± g ) ( x ) = f ( x ) ± g ( x ) , x ∈ D (f \pm g)(x) = f(x) \pm g(x), x \in D ( f ± g ) ( x ) = f ( x ) ± g ( x ) , x ∈ D
积 f ⋅ g f \cdot g f ⋅ g
( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) , x ∈ D (f \cdot g)(x) = f(x) \cdot g(x), x \in D ( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) , x ∈ D
商 f g \frac{f}{g} g f
( f g ) ( x ) = f ( x ) g ( x ) , x ∈ D ∖ { x ∣ g ( x ) = 0 , x ∈ D } \left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)}, x \in D \setminus \{ x | g(x) = 0, x \in D \} ( g f ) ( x ) = g ( x ) f ( x ) , x ∈ D ∖ { x ∣ g ( x ) = 0 , x ∈ D }
初等函数
初等数学中的几类函数
在初等数学中已经讲过下面几类函数:
幂函数:y = x μ y = x^{\mu} y = x μ μ ∈ R \mu \in \mathbf{R} μ ∈ R
指数函数:y = a x y = a^{x} y = a x a > 0 a > 0 a > 0 a ≠ 1 a \neq 1 a = 1
对数函数:y = log a x y = \log_{a} x y = log a x a > 0 a > 0 a > 0 a ≠ 1 a \neq 1 a = 1 a = e a = \mathrm{e} a = e y = ln x y = \ln x y = ln x
三角函数:如 y = sin x y = \sin x y = sin x y = cos x y = \cos x y = cos x y = tan x y = \tan x y = tan x
反三角函数:如 y = arcsin x y = \arcsin x y = arcsin x y = arccos x y = \arccos x y = arccos x y = arctan x y = \arctan x y = arctan x
以上五类函数统称为 基本初等函数
由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数,称为 初等函数
y = 1 − x 2 y = \sqrt{1 - x^2} y = 1 − x 2 y = sin 2 x y = \sin^2 x y = sin 2 x y = cot x 2 y = \sqrt{\cot \frac{x}{2}} y = cot 2 x
等都是初等函数。
本课程中所讨论的函数绝大多数是初等函数。