导数的概念

导数的定义

设函数 $y = f(x)$ 在点 $x_0$ 的某个领域内有定义, 当自变量 $x$ 在 $x_0$ 处取得增量 $\Delta x$（点 $x_0 + \Delta x$ 仍在该领域内）时, 相应地, 因变量取得增量 $\Delta y = f(x_0 + \Delta x) - f(x_0)$;

如果 $\Delta y$ 与 $\Delta x$ 之比当 $\Delta x \to 0$ 时的极限存在, 那么称函数 $y = f(x)$ 在点 $x_0$ 处可导, 并称这个极限为函数 $y = f(x)$ 在点 $x_0$ 处的导数, 记为 $f'(x_0)$，即

$$f'(x_0) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$

也可记作

$$y' \Big|_{x = x_0}, \quad \frac{dy}{dx} \bigg|_{x = x_0}, \quad \text{或} \quad \frac{df(x)}{dx} \bigg|_{x = x_0}$$

导数的几何意义

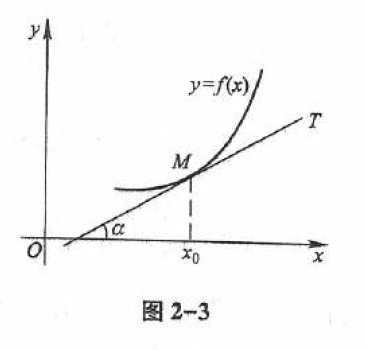
函数 $y = f(x)$ 在点 $x_0$ 处的导数 $f'(x_0)$ 在几何上表示曲线 $y = f(x)$ 在点 $M(x_0, f(x_0))$ 处的切线的斜率，即

$$f'(x_0) = \tan \alpha,$$

其中 $\alpha$ 是切线的倾角（图 2-3）。

如果 $y = f(x)$ 在 $x_0$ 处的导数为无穷大， 那么这时曲线 $y = f(x)$ 的割线以垂直于 $x$ 轴的直线 $x = x_0$ 为极限位置， 即曲线 $y = f(x)$ 在点 $M(x_0, f(x_0))$ 处具有垂直于 $x$ 轴的切线 $x = x_0$（参看同济高数第 80 页例 10）。

根据导数的几何意义并应用直线的点斜式方程，可知曲线 $y = f(x)$ 在点 $M(x_0, y_0)$ 处的 切线方程 为：

$$y - y_0 = f'(x_0)(x - x_0).$$

过切点 $M(x_0, y_0)$ 且与切线垂直的直线叫做曲线 $y = f(x)$ 在点 $M$ 处的 法线 ，如果 $f'(x_0) \neq 0$，法线的斜率为： $-\frac{1}{f'(x_0)}$ 从而 法线方程 为：

$$y - y_0 = -\frac{1}{f'(x_0)}(x - x_0).$$

函数和可导性与连续性的关系

可导必连续 连续不一定可导

---

导数的特定取值表示法

在数学分析和微积分中，导数用于描述函数的变化率。常见的表示方式之一是使用竖线符号来表示特定点处的导数值。

1. 基本表示法

对于一个函数 $y = f(x)$ ，它的导数 $f'(x)$ 表示为：

$$f'(x) = \frac{dy}{dx}$$

当需要计算导数在某个特定点 $x = a$ 处的值时，通常使用竖线符号：

$$k = f'(x) \Big|_{x=a}$$

这表示先求出函数的导数 $f'(x)$ ，然后将 $x = a$ 代入计算其具体数值。

2. 示例

假设函数：

$$f(x) = x^2 + 3x + 5$$

首先计算其导数：

$$f'(x) = 2x + 3$$

如果要求在 $x = 2$ 处的导数值，使用竖线表示法：

$$k = f'(x) \Big|_{x=2} = 2(2) + 3 = 7$$

即该函数在 $x = 2$ 处的瞬时变化率（切线的斜率）为 7。

3. 适用场景

这种表示法在数学、物理和工程学中广泛使用，尤其在以下场景中：

• 切线斜率计算：确定曲线在某点的斜率。
• 运动学：求某一时刻的速度或加速度。
• 优化问题：计算极值点的导数值。
• 微分方程：求特定点的导数初始条件。

4. 其他变体

除了基本的竖线符号外，还有一些常见的变体：

• 二阶导数：

  $$f''(x) \Big|_{x=a}$$

  表示在 $x = a$ 处计算二阶导数。

• 偏导数（用于多元函数）：

  $$\frac{\partial f}{\partial x} \Big|_{x=a, y=b}$$

  表示对 $x$ 求偏导数后，在 $(a, b)$ 处取值。